图集打包策略
二维矩形装箱问题
除了小图集打包入大图中,最近还遇到一个类似的应用情况,那就是三角洲行动里面的背包系统。这个游戏的整理功能非常强大,可以手动触发也可以在拾取物品时自动触发整理,而且三角洲行动中的背包种类多样,形式也不一定是一个完全矩形,此外每个物品还会有优先级问题,比如消耗品要优先放在子弹挂中,珍贵的收藏品要优先放在保险柜中等。而且最牛的是在游戏中这个算法运行起来都是一瞬间发生的,所以我认为这是一个很值得研究的算法。
经典实现——二叉树&第一次适配算法
启发式算法的一种,理论上不一定为最佳适配
在每次循环起始,将一个最大的矩形放置在左上角,然后空间就会这样分成两个小矩形。再次针对小矩形进行递归,这样的算法可以通过二叉树来进行实现。
如果说待排布的矩形按照大小排列,那么就能保证在递归的过程中一直保持二叉树的结构性质。当然排序本身就是一件十分消耗性能的事情,所以也有一些其他的用准确度换性能的算法。
对于二叉树划分本身,可以分为“水平划分(如图)”、“垂直划分”和“最小残余划分”策略。将矩形左上角的点位坐标,空位宽度、长度都存储为一个数据结构当初树的实际存储结点。
在进行二叉树遍历的时候会涉及到选择哪一个矩形来放置的问题,这里也使用启发式的方式来进行推断:
- Best-Fit:贪心算法,优先选择可以容纳新矩形且剩余空间最小的槽
- Worst-Fit:直接选择剩余空间最大的槽,来减少空间碎片
- Best-Wfit:先尝试贪心算法,如果没用合适位置,那么就采用Worst-Fit算法
三角洲行动里面的物品格子是标准化的矩形,不会出现图集这样的非常极限长宽数据。所以这里推测只占一格或者比较小的物品应该是单独进行了补充排列,设置了补充机制来进行排布。
对于已经排列好矩形大小顺序的算法,这种策略叫做离线打包,而实时拿到一个矩形直接进行装箱的算法,这种叫做在线实时打包。离线式的方式,以矩形长宽来划分又分为多种分支策略:
- Bssf:最短边匹配,最短边排列,依次筛选最短边匹配的矩形优先排列,这样的做法能减少空间碎片。
- Baf:最佳空间适配,排列面积,选择剩余空间面积最匹配的位置进行放置,适合大面积填充。
- Blsf:最长边匹配,对长方形适应性友好。
性能优化算法——天际线算法
原网站https://jvernay.fr/en/blog/skyline-2d-packer/implementation/?utm_source=uwl.me
skyline算法不需要对原图像进行提前排列,他是一种在线打包算法。
该算法只关注矩形上界轮廓,所以叫做天际线算法。
数据结构
天际线为一个坐标数组,记录一系列可容纳空间的左下角点位。
更新与特殊情况
初始点位默认为空位矩形的左下角点位,新加入的矩形有一个长宽数据,此时几乎每一个天际线点位都能成为矩形的锚点位。此时需要开始进行点位筛选:
- 排除经计算后矩形过界的点位。
- 如果发生天际线碰撞,则升高矩形以适配最高天际线。
for(int i = 0;i<count;i++){
int x = sky[i].x;
int y = sky[i].y;
//省略过界判断
int xM = x + width;
int i2 = i+1;
//检测是否发生天际线碰撞
for(i2 = i+1;i2<count;++i2){
if(xM<=sk[i2].x){
break;
}
if(y<sk[i2].y){
y = sk[i2].y;
}
}
}
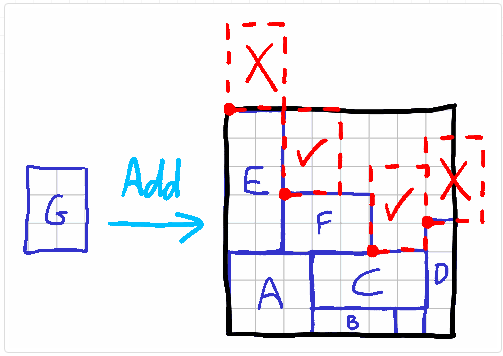
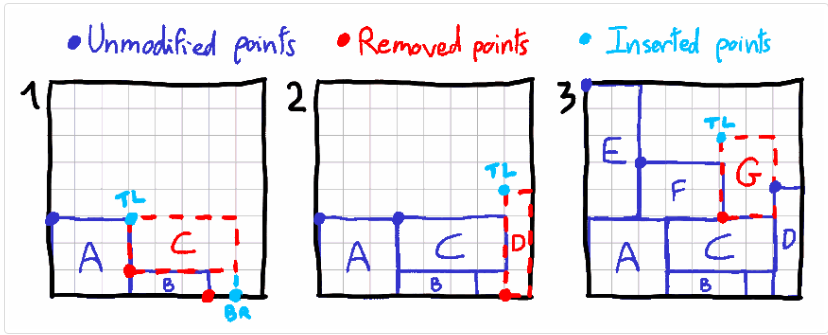
如果新矩形只覆盖一个天际线点,说明是一个“好点位”,那么不需要做更多处理,将此点位纳入候选点位。如果最终被选中,则更新点位为新矩形的左上点位。
如果新矩形覆盖两个或以上点位,说明发生了天际线越界或者天际线碰撞的情况
- 天际线越界的情况不需要做更多处理,可以纳入候选点位。如果被选中。则更新点位为新矩形的左上点位,并将所有覆盖的点位全部去除,更新一个新点位为矩形右边界的下部天际线位置。
- 天际线碰撞的情况做矩形上升。如果被选中,则更新点位为新矩形的左上点位。
点位更新后,还需要判断点位是否和天际线重合,如果是,则去除该点位。
从伪代码中得知该算法有两个嵌套循环,但是循环的次数取决于矩形的宽度,如果宽度越大,则说明点数越小,循环次数可能越少。

