题外话:HPB与欧拉角与万向锁
如果让你去定义一个物体在世界中的朝向信息,你会如何去定义?
邮点问题
万向锁本质并不难,难的是如何解释他,特别是现在众多博客,描述重点并不清晰,亦或者是过于书面化、抽象化,导致读者理解起来十分困难。
很多人在听到这个名词的时候可能还没有遇到和万向锁相关的旋转问题,那么我们先从以下场景开始入手:
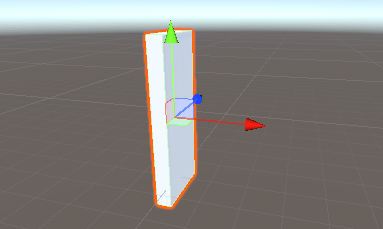
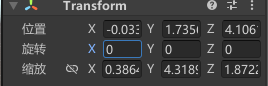
打开unity添加长条物体,并保证初始的xyz轴角度都为0,现在的视角特地调整到比较好理解的角度:红色为x轴,绿色为y轴,蓝色为z轴——于此同时这个“物体坐标轴”是和世界坐标轴是相对应的。
我们先初始定义两个概念
- 静态坐标系——可以对应上世界坐标系,也就是物体的改变影响坐标系本身,物体的变换严格遵守这个坐标系的参照。
- 动态坐标系——坐标系与物体牢牢“焊死”,方向随着物体同步改变。
欧拉角描述的就是动态坐标系的旋转。
欧拉角:用于计算空间中刚体的旋转位置,目的是改变刚体的朝向。欧拉角的大小描述的是结果而不是过程——这句话非常重要,在之后的理解中帮助很大
这个神奇的“旋转”属性乍一看似乎很容易理解——”不就是绕xyz轴旋转“
但只要读者看过我前文的两个概念,就难免会产生一个新的疑问——“这个属性到底是描述的静态坐标系,还是动态坐标系?”
我们试着先将x改为90度,发现物体正常绕x轴旋转了90度,从这里看似乎还分辨不出坐标系:
然后再将y改为90度,红色的坐标轴(x轴)对准了屏幕:
对于物体身上的静态坐标轴,物体是绕着“z轴”转的,也就是说这个旋转似乎是以世界坐标轴为依据。
然后我们又将z改为90,匪夷所思的事情发生了,物体按照原来改变y的值的路径重新转了回去。
虽然图是复制过来的但事实就是如此,不信读者可以自行上号unity验证
看来事情远远不止这么简单,,,,,,
half-time
Q:既然属性的机制如此复杂麻烦,那为何不直接使用静态坐标系来当旋转基准呢?
A:可以从最肤浅的角度来理解,直接使用世界坐标系确实是一个简单的方法,在unity的实际操作中确实有很多直接运用世界坐标系对物体直接进行旋转的手法,但设想一下,假如我们要使用角度来描述飞机运动,那么此时此刻的角度描述是否直接通过自身坐标系会更好呢?——其实不是,我口嗨的
邮点思考
首先我们可以确定的是,这个xyz轴属性本身只是一个物体在空间中的信息,它并不代表物体的实际旋转,或者说没有直接关联。
比如在场景中直接启用旋转工具,手动控制物体旋转,会发现偶尔会出现调整一条坐标轴却三个属性都变换的情况。
读者应该对这样一个东西很熟悉:
万向地球仪
unity的Transform中的旋转的具体值,其实就是欧拉角的值,如果你还是对欧拉角感到陌生,那么可以直接将它理解成这样一个地球仪。
这样的地球仪有一个很大的特点,就是旋转轴是一层套一层的,可以看见在旋转最外层的旋转轴时,里面所有的结构都会随之旋转。
这个时候应该对欧拉角有一个初始的印象了,unity中的欧拉角轴,就是按照这种形式来旋转的,而且y轴在最外层,x轴其次,z轴在最里层。
为什么要这样设置呢,其实笔者在各大网站上寻找观点的时候,并没有找到符合笔者心理预期的“答案”。
于是笔者索性简单地猜测了一下:这样的设置缘由,应该只是为了响应计算机对于图形旋转的处理。
这句话也比较抽象,如果读者对计算机图形学还没有了解,那可以先看:
空间变换 | Coding中。。。 (jiuriri.com)
光栅化与抗锯齿浅入 | Coding中。。。 (jiuriri.com)
以unity为例,计算机在处理物体旋转的时候,都是通过将物体上的某点的位置信息做成矩阵,然后再通过这个矩阵与其他旋转矩阵相乘,最后得出的新矩阵作为旋转后信息。
从GAMES101-现代计算机图形学入门-闫令琪哔哩哔哩bilibili得知,计算机在进行实际计算时,旋转矩阵是理解成三个轴分别进行旋转矩阵相乘,再组合成一个旋转矩阵来进行最终相乘。
写在原文章中的:
Rxyz(a,b,c) = Rx(a)Ry(b)Rz(c)
但是不用在乎这个式子的顺序,其实只是相表达旋转矩阵是由三个轴的旋转矩阵一步一步相乘得来的
我们还可以从中得知静态坐标系各个变换顺序的旋转矩阵是左乘的,动态坐标系各个变换顺序的旋转矩阵是右乘的。
这里就不详细讲了
然后我们再试想这样一种情况:早上八点早起下床,那么下床这个动作可以用两种方法来实现。
- 一种是先坐起来,然后”向左转“下床——x轴-90度,z轴-90度
- 一种是先”向左翻“,然后身体侧着坐起来下床——y轴-90度,z轴-90度
试想以头向上为y轴,面朝向为负z轴的左手坐标系
最终得出的结果都是一样的,但过程其实不一样。
从上我们可以得出什么信息呢?
- 计算机需要一步一步进行计算
- 计算机每一步进行计算后,整个坐标系都会根据计算结果发生改变
这是什么东西?没错,就是他:
half-time
Q:为什么三个轴不一起旋转呢?
A:有两个原因:1、这个已经解释过了,计算机的计算是一步一步来的;2、这个也许更接近本质,我们都知道物体旋转的时候轴会发生变动,那么同时旋转轴最终旋转的结果就不是我们设想的那样了——如果有模拟飞行游戏,你可以试试命令飞机一直“向右下飞”,最终的结果是飞机在天上螺旋式旋转!
邮点启发
假设绕y轴旋转为heading,绕x轴旋转为pitch,绕z轴旋转为bank(有点类似空间变换 | Coding中。。。 (jiuriri.com)中飞机旋转模型),则先heading45°再pitch90°等价于先pitch90°再bank45°。
再联想我们之前说过的重点
欧拉角的大小描述的是结果而不是过程
经过一次又一次的强调,你是不是已经初步开始忽视欧拉角的值了呢,没错,欧拉角只是用来描述图形旋转完成后的终极朝向,而不是在描述一个图形按照什么什么方式进行旋转。简单地说,一种旋转情况可能能解出两组甚至多组欧拉角解。
而万向锁是什么,想象一下上面那个地球仪,其实图片所示的情况就是万向锁的情况,如果我们将地球仪沿最外层旋转,和将最内层的地球进行旋转,那么得出的结果都是”水平地旋转地球“。
在unity中将一个默认的物体x轴欧拉角旋转90度,那么调整y轴欧拉角和调整z轴欧拉角得出的结果将是一样的,这就是万向锁——他将一个方向的维度给丢失了。
为了保证任意方位都只有独一无二的表示,Unity引擎限制了角度范围,即沿x轴旋转限制在 -90 ~ 90 之间,沿 y 与 z 轴旋转限制在 0 ~ 360 之间。
欧拉角带给我们什么?它可以只使用三个数,就能够表示物体在空间中的旋转情况。缺点是什么呢,我们在旋转的过程中,再次进行欧拉角的调整往往不会向着我们预想的情况进行,更何况还有万向锁的情况发生。
欧拉角的工程应用:飞行器姿态控制、量子力学、刚体坐标系等......
邮点结论
看来我们要放弃通过直接变动这个属性来实现物体旋转的想法了😦!
比如说,如果要在代码中描述物体旋转,我们也许使用以下的方式更好些:
- 使用旋转矩阵——可见空间变换 | Coding中。。。 (jiuriri.com)
如果要避免万向锁,我们也可以尝试这样:
- 限制旋转角度——这个unity默认做到了
- 改变旋转顺序