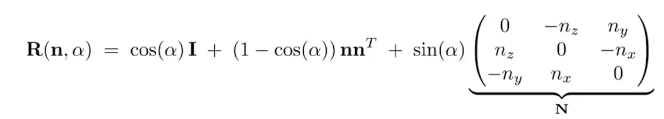空间变换的意义
模型变换
- 描述摄像机运动
- 描述模型运动
视图变换
- 3D到2D的投影变换
二维变换
刻度矩阵
x`=sx
y`=sy
写成矩阵：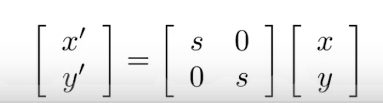
叫做缩放矩阵
- y轴反转：
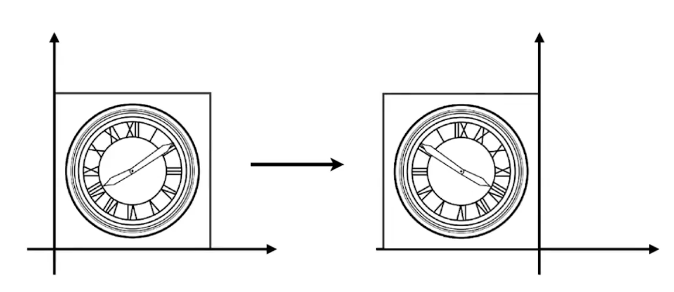
x`=-x
y`=y
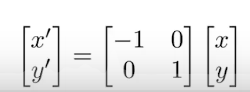
- 斜变化：
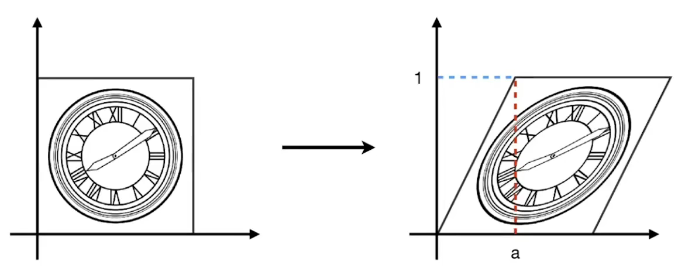
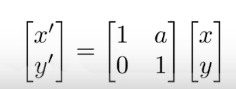
- 旋转变化：
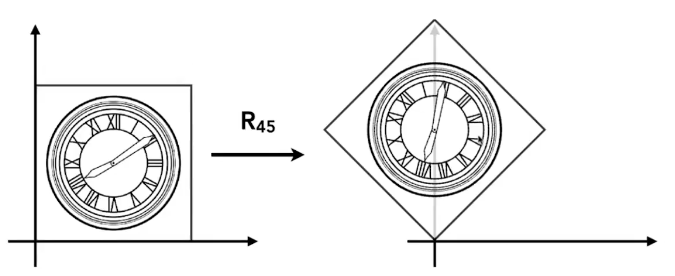
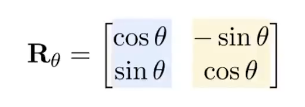
将特殊点代入就可以算出来
没有额外交代，旋转永远以原点为旋转中心
齐次坐标
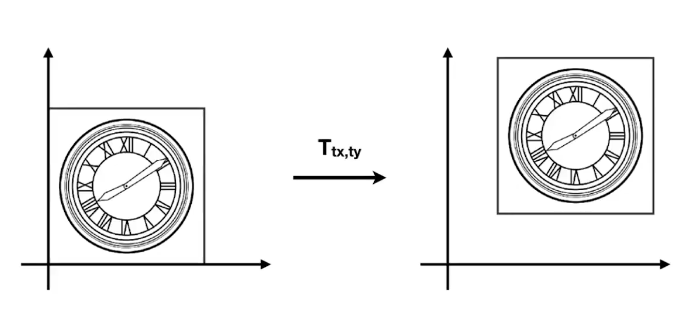
并不能用上述说的矩阵表示
于是
- 2D point =(x,y,1)T
- 2D vector =(x,y,0)T
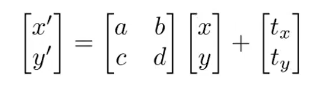
但是不是线性变换，不满足”由一个矩阵变换而来“的约定俗成格式
所以引入一个新坐标
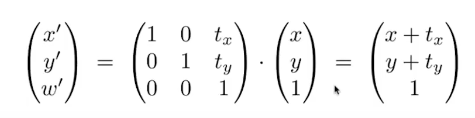
解释如下：
- vector + vector = vector
- point - point = vector
- point + vector = point
- point + point = ??
两点相加其实是中点
其实所有二维点(x,y,w)T最终都能变换成这样的形式(x/w,y/w,1)T
然后为什么坐标后面增加的是1，而向量后面增加的是0呢？首先看结果，进行平移变换后，点的坐标是满足我们需求的，而向量的特点是”平移不变“，所以我们不应该在进行平移操作后改变向量的值，所以0是用来保护向量的
特点：在二维情况下的仿射矩阵中，最下面一排必为001
- 逆变换：
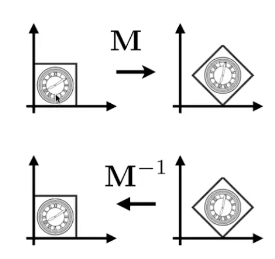
变换回来的方法就是乘以逆矩阵
有意思的是对于旋转变换来说，他的逆变换就是向反方向旋转相同角度，而反方向旋转矩阵就是正方形旋转矩阵的转置，所以说对于旋转矩阵，他的转置就等同于他的逆（数学上叫正交矩阵）
组合变换
- 复杂的变换通过简单变换组合得来
- 简单变换的顺序很重要（很形象：矩阵乘法不满足交换律）
于是：
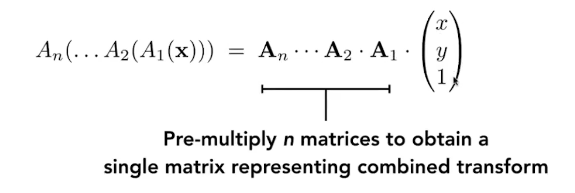
从右到左
可以说，一个3X3的矩阵，可以代表很多变换的组合，这就是这个矩阵很神奇的地方，无论多么复杂的变换，通过这个小小的3X3矩阵就能够表示
实战：
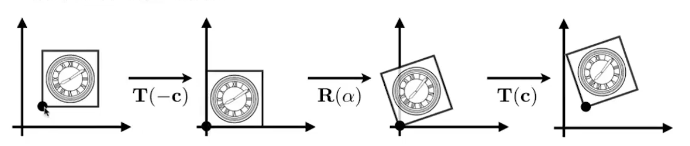
非原点的旋转如何实现？很难写，那么可以先把这个点移动到原点，平移过去后再进行旋转，这就是逆向思考，反过来分解矩阵
三维变换
依葫芦画瓢
- 3D point =(x,y,z,1)T
- 3D vector =(x,y,z,0)T
同样多一个齐次坐标
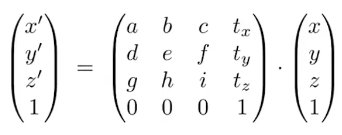
对于三维物体变换来说，难点在于旋转
- 绕轴旋转变换
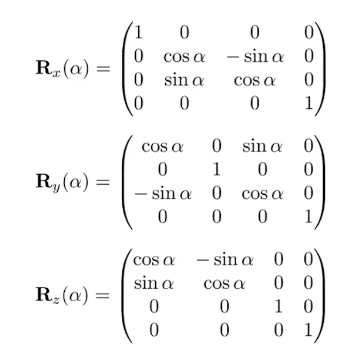
分别代表绕某条轴旋转
- 普遍旋转
Rxyz(a,b,c) = Rx(a)Ry(b)Rz(c)
飞机三大基本旋转：roll、pitch、yaw
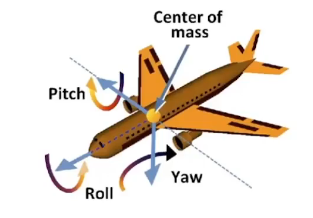
罗德里格斯旋转公式
//
观测变换
View/Camera Transformation
回忆一下现实生活中拍照片的过程
摆造型->选角度->拍
观察变换，就是“选角度”的过程
投影变换
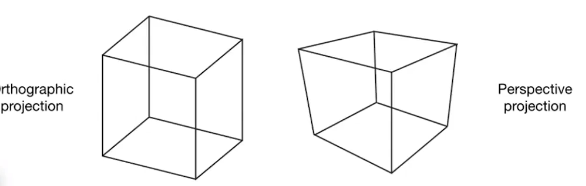
其实这个可以见//cinemachime基本操作//
那就不细聊原理了
正交
实际上投影的实质是从相机空间到裁剪空间的变换：
- 将相机摆放到原点，布置好方向，朝向等
- 去除z轴（会出现无法区分物体前后的情况）
- 按比例移动并拉扯成到[-1,1]2的矩形上（转换为规范视域体，为了方便处理，无需考虑屏幕尺寸）
实质操作
- 用AABB包围盒（6个参数）转换为规范视规体
OpenGL为(-1,-1,-1)到(1,1,1)
DirectX为(-1,-1,0)到(1,1,1)
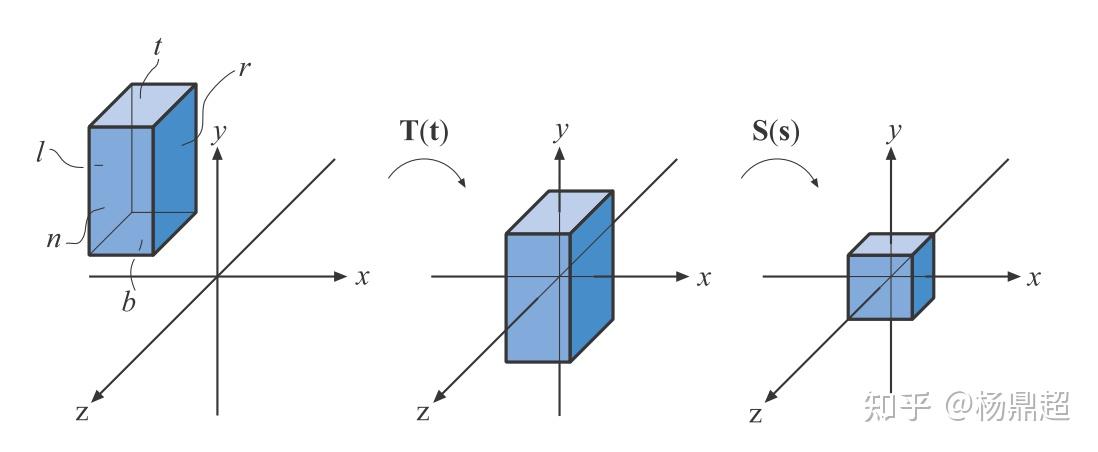
在三维上，由于常用右手系坐标，所以远近在z轴上表示是远比近小（比如x轴是远比近大，是完全相反的
图片来着知乎@杨鼎超
透视
先导复习：点(1,0,0,1)与点(2,0,0,2)在三维中其实代表一个点
实质是把一块空间中所有点，各自按照一定角度形成线状”挤“入屏幕中
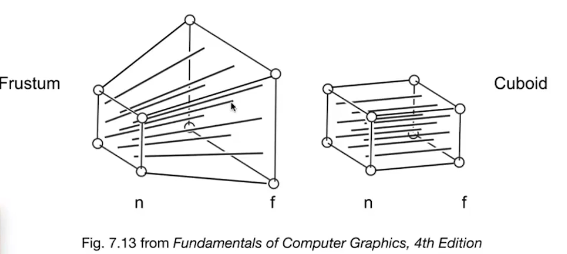
细说如何变换：
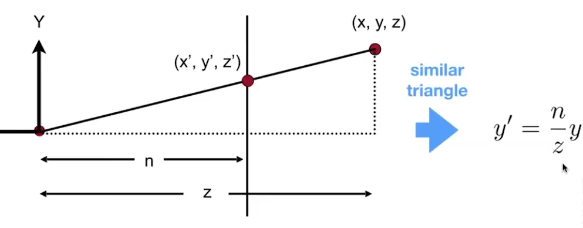
颇有一种土木老哥测距内味儿
将某个点的变换写成齐次矩阵性质：
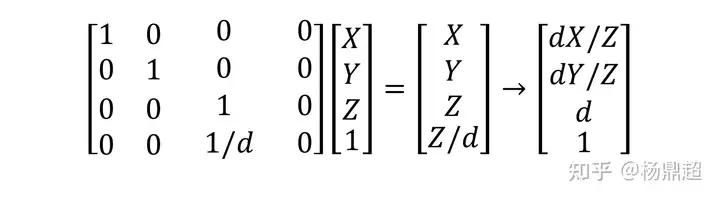发现问题：Z不见了，发生了和正交一样的情况
于是变换一下思维，可以先把这个锥体（视锥体）变为AABB包围盒，再转变成规范视规体（如上上图所示）
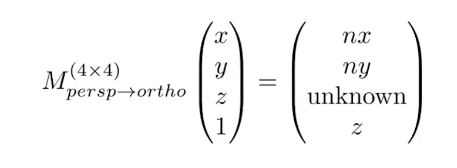
矩阵计算方法如下：
- 统计所有常规点位变换规律（就是上图）
- 统计近裁面上的所有点（也就是(x,y,z,1)T=W(x,y,z,1)T)
- 统计z轴上的点，z轴值不变
解方程最终结果为：
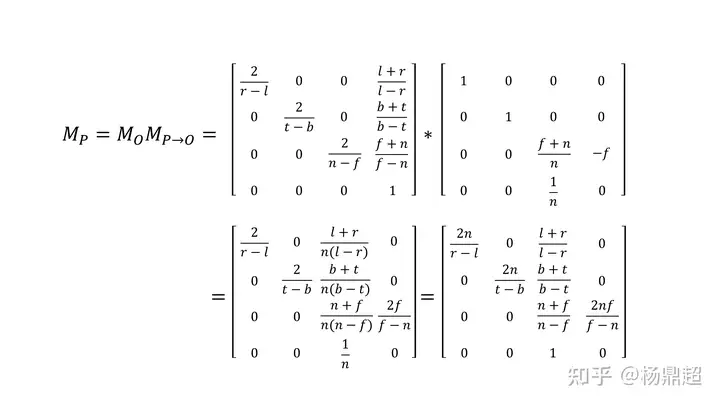
图片分别来自知乎@杨鼎超与BiliBili@闫令琪