动态规划の一句话解释
要点:列出额外空间(通常是哈希表等)来储存计算后的结果,当再次遇到相同计算时直接查表,这样就能剩下大量重复计算的时间,是一种空间换时间的算法。
实现方法:将待求解的问题分解成若干子问题,先求子问题的解,在反过来得出总问题的解。
实现步奏:
- 找出最优解的性质,并刻画其结构特征
- 递归定义最优解
- 以自底向上的方式计算最优解(求出最优值)
- 构造最优解(求出最优解)
简单引入例
一列序列如下,找出最长的递增的子序列长度:
1,5,2,4,3
先用肉眼观察,最长的子序列应该是123或者124
人脑子算起来很方便,对于处理这种简单数据,人脑会本能地自动对123这个顺序列“标记重点”,但对于机器他只能一个一个数去进行对比
反正,最终得出的答案肯定是某个从第i个数开始到第j个数截止(那么肯定包括i和j)的从小到大的顺序列,所以直接定义从i开始到j的递归函数
int L(nums,i){//定义输入操作数组本身和操作数i
if(i==sizeof(nums)) return 1;
int max_len=1;//最小为1,所以最大的长度为1
for(int j=i+1;j<sizeof(nums);j++){//重复检查i之后的所以数据
if(nums[j]>nums[i]){//找到第一个符合条件的数
max_len=max(max_len,L(sizeof(nums),j)+1);
//将这个数设为操作数i并重新引用自身函数进行递归,找出下一个符合条件的数
}
}
return max_len;//返回的就是下一个递归的i
}
上述函数的作用是给出从i开始的数组最长子序列,所以之后我们再将所有数i代入计算出最大的哪个数就是答案
int length(nums){
int max_len=1;
for(int i=0;i<sizeof(nums);i++){
max_len=max(L(nums,i),max_len);
}
return max_len;
}
从上述函数可知,我们用L函数得出从i到后面所有数的“最优解”,再用length函数改变i的值,从而算出所有从i到j的所有结果!
写算法确实爽,计算机开算CPU可能真得烧了,因为这两个函数叠一起时间复杂度竟到达了惊人的
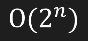

这是一个非常恐怖的时间函数,以正常使用的计算机算法中,n^2已经算是比较缓慢的算法,而这个暴力拆解居然达到了恐怖的指数级!
这个反常识的时间算法是怎么得出来的呢?从所有的i到所有的j的计算,计算机会尝试将所有的i和j给代入然后运算出来,意味着计算机会出现大量的重复计算,比如从第三个到第五个数的计算中包含从第三个数到第四个数的计算,但计算机计算第三个数到第四个数的时候,不会对计算结果进行记忆,还是会傻兮兮地再算一遍😂
那我们再通过人工干预让他记住计算结果呗,于是我们引入二维数组A【i】,用于记忆从i开始的最长长度。
#int A[5];
int L(nums,i){
#if(A[i]!=NULL){
return A[i];
}
if(i==sizeof(nums)) return 1;
int max_len=1;
for(int j=i+1;j<sizeof(nums);j++){
if(nums[j]>nums[i]){
max_len=max(max_len,L(sizeof(nums),j)+1);
}
}
A[i]=max_len;
return max_len;
}
加#号为增添的代码
由于递归对计算机的性能有较大要求,现再写一份非递归的
int length(nums){
int n=sizeof(nums);
int L[5]={1,1,1,1,1};
for(int i=4;i>0;i--){
for(int j=i-1;j>0;j--){
if(nums[j]>nums[i]){
L[i]=max(L[i],L[j]+1);
}
}
}
return *max_element(L,L+5);
}
非递归的算法显然地表示了时间复杂度为O(n^2)
以上例子,明显可以看出解出问题的结构是符合一般结构的
- 是某个数i到某个数j之间的顺序数列(数字特征,列出后可以用机器方式量化数据)
- 递归法写出算法
- 迭代法写出算法
当然如果需要更详细的信息,则进行步奏4
基本要素以及01背包
- 最优子结构
在动态规划算法中,利用问题的最优子结构性质,以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。在算法中,其子问题往往规模非常小,例如上例所说的“比大小”为最小算法层次,整个算法比了n^2次大小,则时间复杂度就为O(n^2)
- 重叠子问题
即反复重复计算的子问题只解一次,然后将解存入表格中。当再次需要解此子问题时,只需要用常数时间查看一下表格即可