初识黑红树
234树
234的含义指一个节点可能含有的子节点个数
规则:非子结点的子节点数总是比它含有的数据项多1
结点所含数值编写规则有点类似普通树的中序遍历 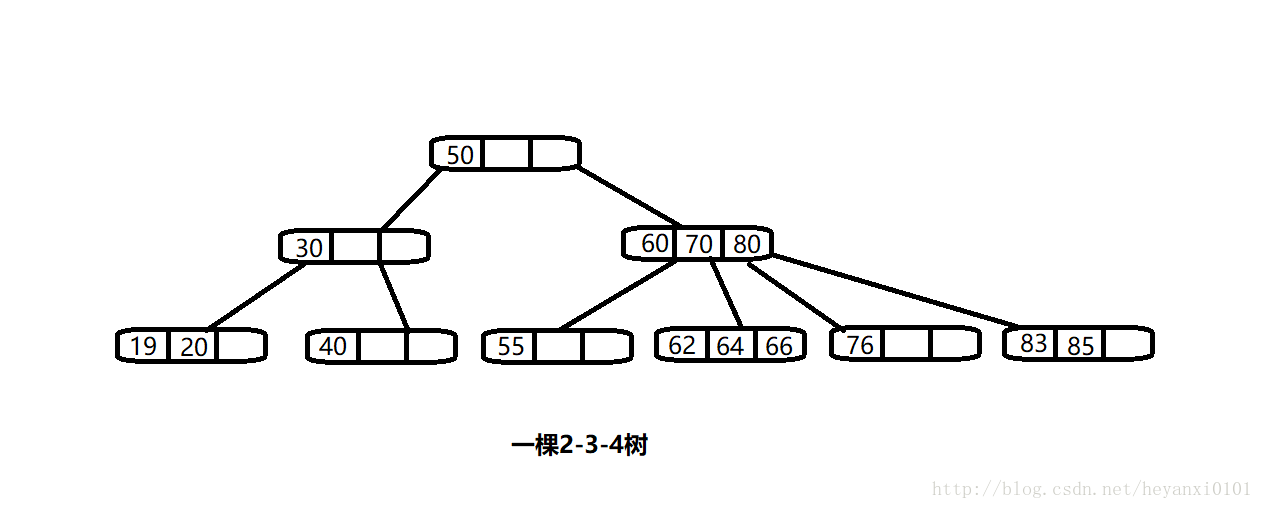
234树的插入
- 当插入节点没满数据,时,直接插入,可能需要移动一到两个数据
- 若插入节点已满,则需要进行节点分裂来保证234树的平衡//AVL树//
一般情况下,分裂的规则一句话概括就是“将中间数据往上提”
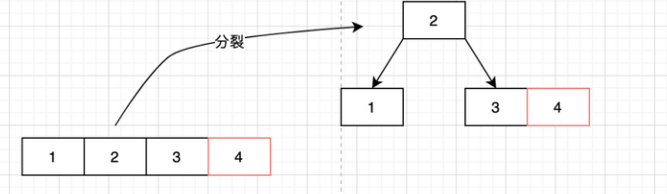
但是在多次插入或者插入已知树时,遇到没满节点,需要先插入满其子节点,自身节点需要靠子节点分裂来补充
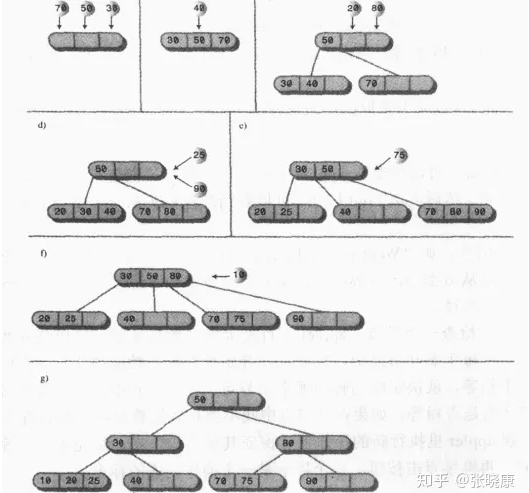
//代码在代码特殊训练中补//
##黑红树与234树
黑红树就是234树的另类表示方法
黑色节点与红色节点结合起来表示234树中的节点
规则如下:
- 2节点->黑色单节点
- 3节点->黑色节点接红色节点(在我目前学习过程中默认左倾)
- 4节点->黑色节点接两红色节点
特殊黑红树:23树所建立的黑红树(都为左倾红节点,在很多地方简化黑红树的复杂性,所以一般情况下的黑红树优先考虑23树)
黑红树特性(官方特性)
- 节点颜色有黑有红(不是废话?)
- 根节点必为黑色(感觉也是废话)
- 所有叶子节点都是黑色(实际情况下这种节点是空节点)
- 任意节点到叶子节点经过的黑色节点数目相同
在23树中,对应黑红树的黑红节点是同一层的,所以只有黑色节点在贡献高度,反应在黑红树中就是黑色完美平衡
- 不会有连续的红色节点
会产生以下效果:
- 对于二叉树来说,进行查找插入删除的时间复杂度为O(logn),但是不足以抵消维护AVL树的成本
- 时间复杂度是基于树的高度来的,所以说理论上减少树的高度能低成本降低时间复杂度
- 在结点中增加数据显然能降低树高,比如23树,理论上哪怕345678树,结点越高越省
- 难点在于从代码层面上生成富数据结点树,于是将23树转化成黑红树
- 黑红树具有和二叉树一样的结构,能以O(logn)的时间复杂度进行操作,任何不平衡只需三次旋转
插入时
黑红树将待插入节点涂成红色
红色节点的意义:与父节点进行关联
若出现双红色子节点的情况(即4节点树的情况),黑红树需要在插入后进行调整
即树的涂色与旋转
旋转与AVL树中“上提平衡”如出一辙,所以不再多言
先说统计结果(基于左旋黑红树):
1、两红子节点,父节点染红,两子节点染黑
2、连续红节点,若出现与父节点同属性情况,则将三节点上提右旋,并使新父节点染红,再染黑子节点(与1出现交叉定义)
3、连续红节点,若出现与父节点反属性情况,则将两红连续节点左旋,再按照2处理
类似结果在23树中有对应插入方式
删除时
删除首要遵循的规则和二叉查找树通用的删除策略一样,即删除后用前驱节点/后继节点来填充
删除结点导致的最大后果就是有可能改变了树的黑高,前面已经提到过黑红树一种维持黑色结点平衡的情况,所以说删除后的维护也同样重要。
注意代码层面上作为叶子结点的空结点NULL视为黑色
这里分多种情况进行操作,设定要删除结点为v,删除后用来填充的结点为u
先易后难,首先是比较简单的不会改变黑高的情况,那就是u或者v是红色
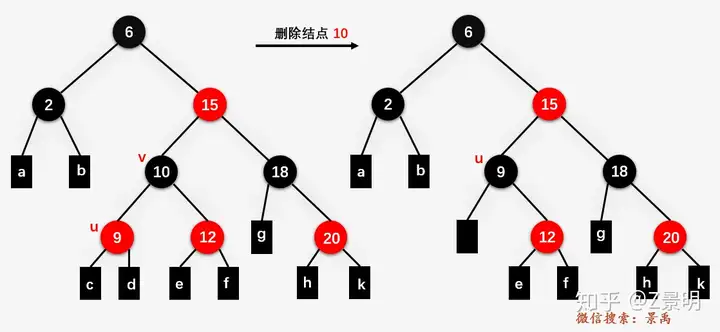
直接将替换后的结点染回黑色
然后是复杂的v和u都是黑色结点的情况了,这里会改变黑高,所以分多种情况表示
v和u都是黑色结点的复杂情况
u是双黑结点且不是根结点
先设定u的兄弟结点为s
s为黑且s的孩子结点至少有一个红色
(1)s和红色子节点(或者孩子都是红色)按照“LL”排列
将s的对应红色孩子染黑,然后右旋转(上提)
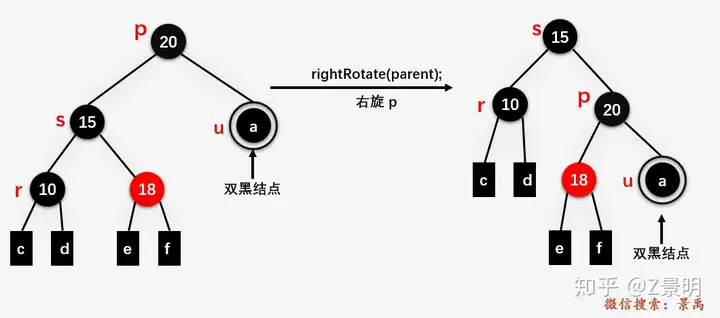
“双黑结点”即受到删除后待处理结点,处理完后变为单黑结点 “双黑”即占用两黑高位
(2)s和红色子节点(或者孩子都是红色)按照“LR”排列
先将相应红色结点染红,然后小左旋,形成LL的情况
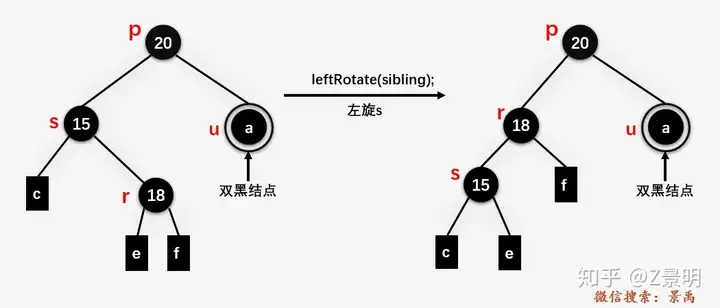
然后和LL一样进行大右旋,平衡黑高
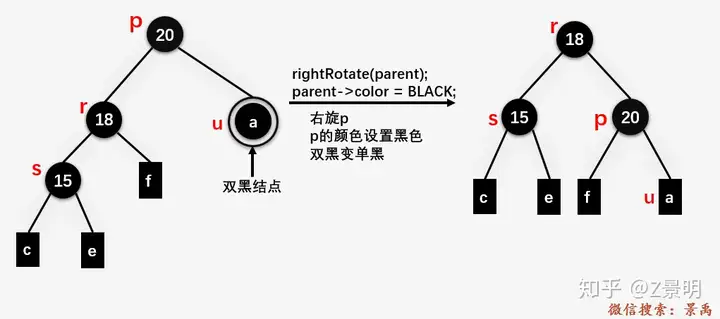
(3)s和红色子节点(或者孩子都是红色)按照“RR”排列
和LL情况相对称,染完色后如图

(4)s和红色子节点(或者孩子都是红色)按照“RL”排列
和LR情况相对称,染完色后如图
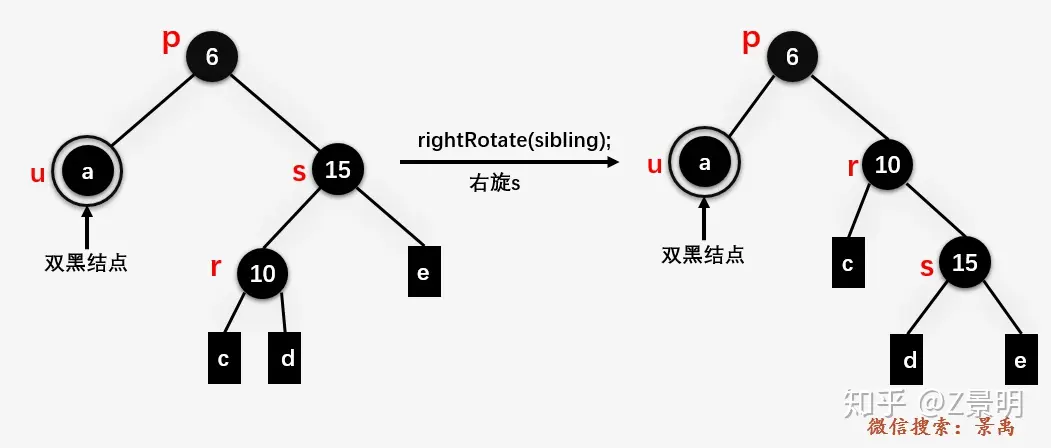
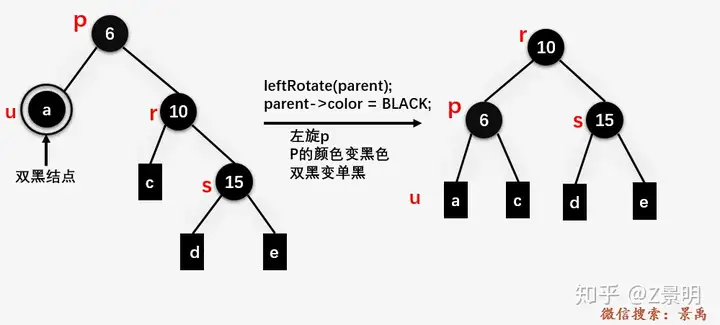
s是黑色且s的两个孩子结点都是黑色
删除后首先将s染红,此时对于父节点来说这个子树达成黑色平衡,但对于整体树来说这个子树少了一树高,所以将父节点标记为双黑结点,即现在开始处理父节点,问题就向上转移向上递归了
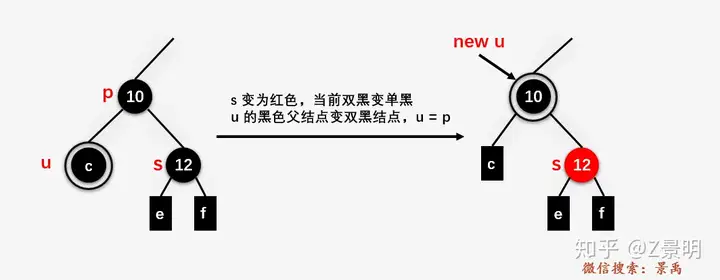
若爷爷结点仍然为黑,则把父节点当作问题结点按黑红树标准规则处理,若一直出现题中情况,则直到递归到红色结点停止(直接将该结点染红,则整体树达到黑红平衡!)
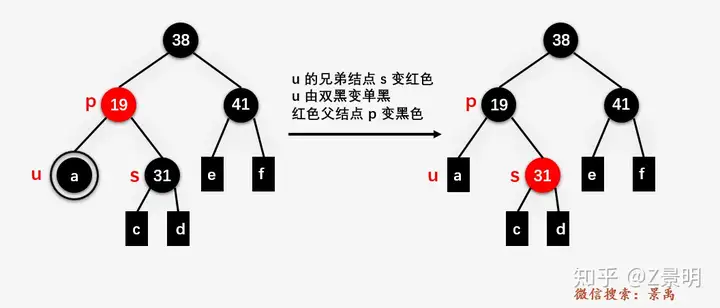
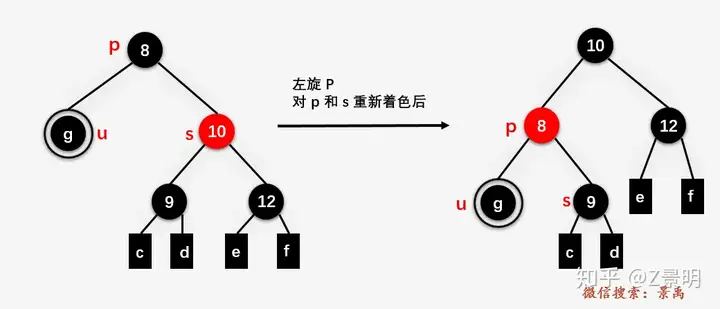
s是红色结点
(1)s是父节点左孩子,对父节点进行右旋操作

注意此时s结点改变对象
发现双黑结点此时形成了 s 是黑色且 s 的两个孩子结点都是黑色的情况
那么直接作相应处理就好,而且父节点恰好就是红,可以不用递归
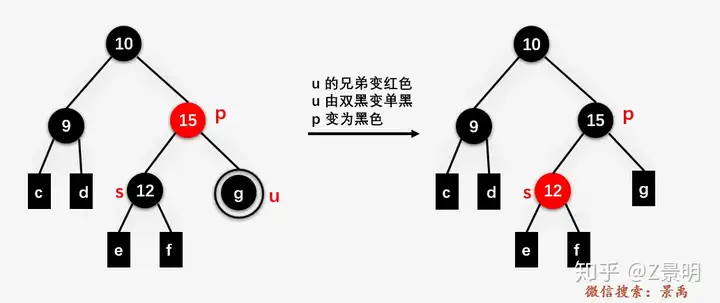
(2)s是父节点右孩子(和上面情况对称罢了)

u是双黑结点且为根结点
直接变单黑就行