AVL树转化规则

定义：
平衡因子BF=Hl-Hr的值绝对值不超过1

高度差越高，查找所需要的平均查找长度就越长，所以要尽量避免高度差

在定义中加入高度属性

class AVLNode<T extends Comparable<T>> {
    private T data;
    //左节点
    private AVLNode<T> left;
    //右节点
    private AVLNode<T> right;
    //当前节点的高度
    private int height;
}

计算高度

int height(AVLNode<T> node){
    if (Objects.isNull(node)) {
        return 0;
    }
    int rHeight = height(node.getRight());
    int lHeight = height(node.getLeft());
    return Math.max(rHeight, lHeight) + 1;
}

即节点左右子树高度的最大值+1为树的高度

平衡调整

插入分为以下四类：
* ADF路径（RR插入）
* GDB路径（LL插入）
* ADB路径（RL插入）
* GDF路径（LR插入）

ADF路径和GDB路径

当插入节点与父节点的属性相同时

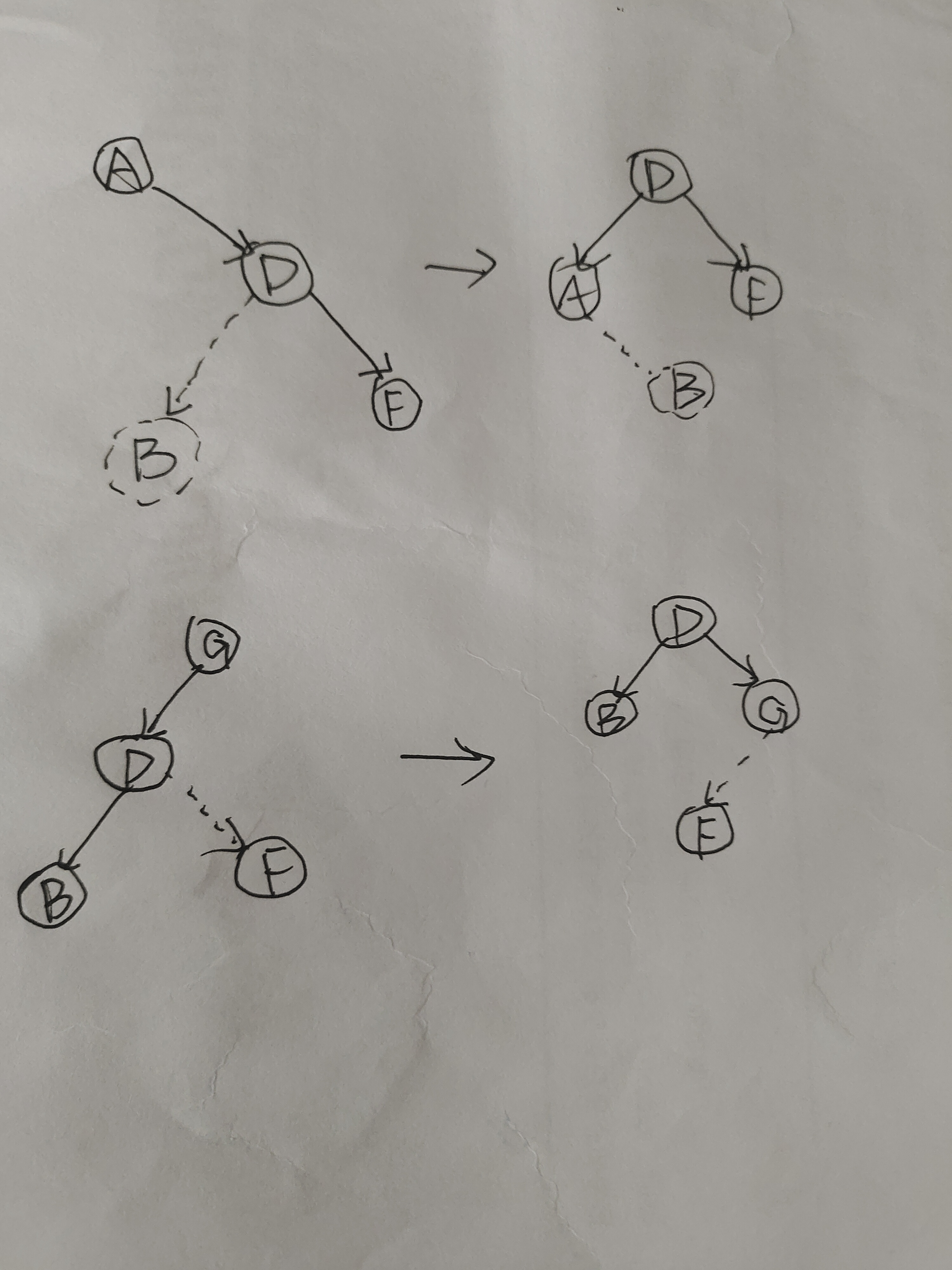
其实就是将中间节点提起来平衡

AVLNode<T> singleRightRotation(AVLNode<T> node) {
    AVLNode<T> result = node.getRight();
    AVLNode<T> left = result.getLeft();
    node.setRight(left);
    result.setLeft(node);
    return result;
}  

AVLNode<T> singleLeftRotation(AVLNode<T> node) {
    AVLNode<T> result = node.getLeft();
    AVLNode<T> right = result.getRight();
    node.setLeft(right);
    result.setRight(node);
    return result;
}

ADB路径与GDF路径

当插入节点与父节点的属性相反时
先将插入节点放入父节点的父路径上，形成ll或者rr后再运用相应转化方法
~~其实不是懒得放图~~

AVLNode<T> doubleRightLeftRotation(AVLNode<T> node){
    AVLNode<T> right = singleLeftRotatio(node.getRight());
    node.setRight(right);
    return singleRightRotation(node);
}  

AVLNode<T> doubleLeftRightRotation(AVLNode<T> node) {
    AVLNode<T> left = singleRightRotation(node.getLeft());
    node.setLeft(left);
    return singleLeftRotation(node);
}

删除节点时的平衡调整

其实和二叉搜索树大同小异 * 叶子节点直接删除
* 包含一个子节点，将子节点替换到父节点
* 包含两个，使用后继节点替换被删除节点，删除后续节点
//代码和详细原理在数据结构复习中补//

参考：微信公众号——javascript艺术